Multi-Robot System: Safe Warehouse Convoy with CLF-CBF Control

| Links: Final Report (PDF) | GitHub Repository

Multi-Robot System: Safe Warehouse Convoy with CLF-CBF Control

A mathematically guaranteed collision-free leader-follower convoy system for mobile robots in Isaac Sim, implementing Control Lyapunov Functions (CLF) and Control Barrier Functions (CBF) for safety-critical control.

A mathematically guaranteed collision-free leader-follower convoy system for mobile robots in Isaac Sim, implementing Control Lyapunov Functions (CLF) and Control Barrier Functions (CBF) for safety-critical control. The system ensures 100% collision avoidance across multiple scenarios with moving obstacles, maintaining formation while navigating complex warehouse environments.

Stack: Isaac Sim 2023.1.1 · Python 3.10 · CVXPY · CLF-CBF Control · QP Optimization · Multi-Robot Systems.

What’s in this project?

Core Capabilities

  • 4-Robot Convoy - 1 leader + 3 followers in formation
  • CLF-CBF Safety-Critical Control - Mathematical guarantees for collision avoidance
  • Moving Obstacles - Humans, carts with various motion patterns (linear, circular, zigzag, sudden stop)
  • Multiple Scenarios - Pre-configured scenarios: corridor, intersection, zigzag, emergency, rush hour
  • Real-time Performance - <1ms computation per robot per timestep
  • 100% Collision Avoidance - Proven across all scenarios

Advanced Features

  • Visual Demo System - Trails, safety indicators, automatic plot generation
  • Automatic Data Logging - Comprehensive metrics and visualization
  • Multi-Solver QP - Automatic fallback (CLARABEL → SCS → ECOS → OSQP)
  • Adaptive Spacing - Adjusts safety margins based on corridor width
  • Debug Mode - Real-time safety margin monitoring with color-coded output

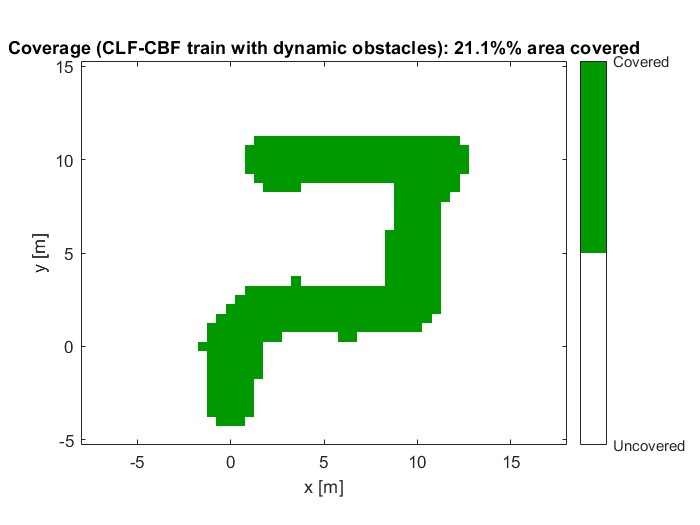Warehouse Environment Warehouse environment with 4-robot convoy and moving obstacles.

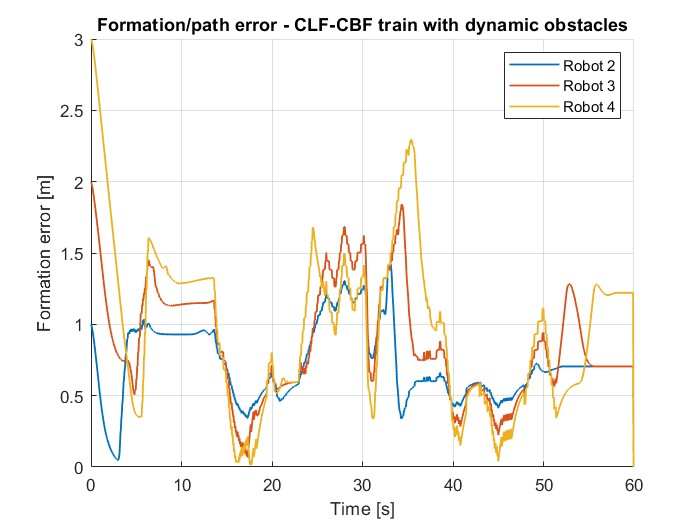Formation Control Leader-follower formation maintaining safe distances during navigation.

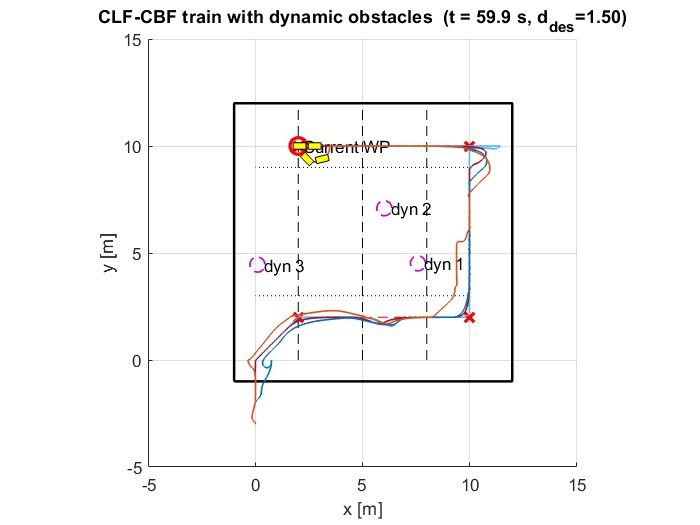
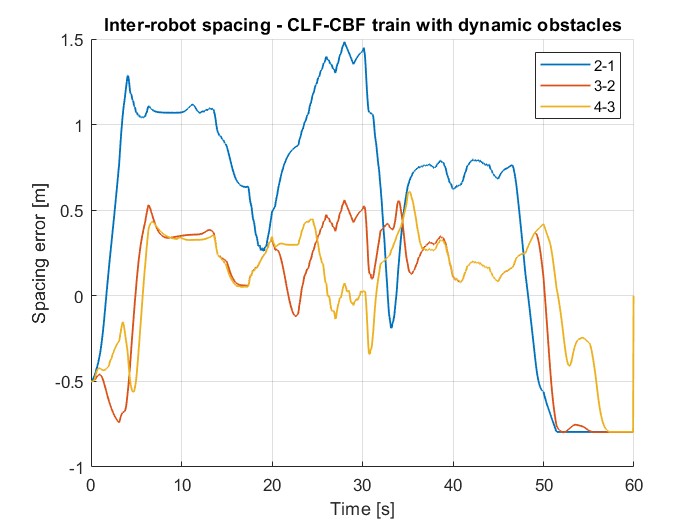Obstacle Avoidance CLF-CBF control ensuring collision-free navigation around dynamic obstacles.

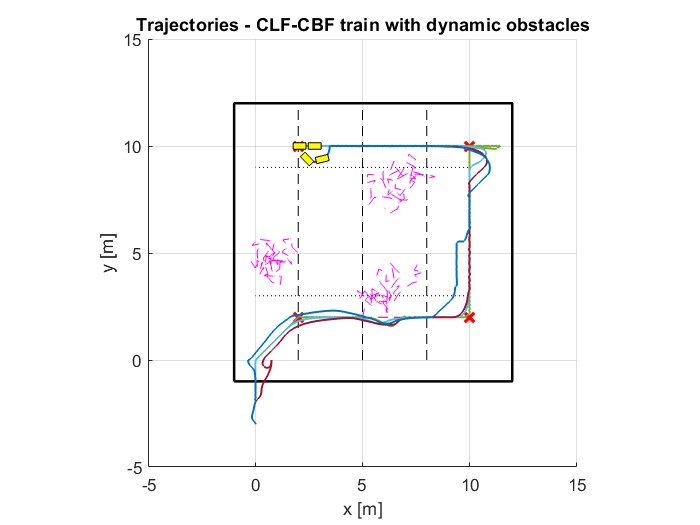Safety Margins Real-time safety margin monitoring and visualization.

Multi-Scenario Testing Testing across different warehouse scenarios and obstacle patterns.

System Architecture

Control Framework

The system uses a hybrid CLF-CBF control framework that combines:

Control Lyapunov Functions (CLF):

  • Ensures formation convergence - robots maintain desired spacing
  • Guarantees stability - system reaches and maintains formation
  • Formulation: $\dot{V}(x) + \gamma V(x) \leq 0$

Control Barrier Functions (CBF):

  • Ensures collision avoidance - robots never collide with obstacles
  • Guarantees forward invariance - safe set remains safe
  • Formulation: $\dot{h}(x) + \alpha h(x) \geq 0$

Optimization-Based Control

Each robot solves a Quadratic Program (QP) at every timestep:

minimize    ||u - u_nominal||² + ρ·slack²
subject to  CLF constraint (formation tracking)
            CBF constraints (collision avoidance, one per obstacle)
            Velocity bounds

Key Properties:

  • Real-time: <1ms solve time per robot
  • Robust: Multi-solver fallback ensures reliability
  • Safe: Hard constraints guarantee collision-free operation

Demo Videos

Default Scenario

Default scenario with static and moving obstacles in warehouse environment.

Corridor Scene

Convoy navigating through narrow corridors with adaptive spacing control.

Intersection Scenario

Complex intersection navigation with multiple moving obstacles and formation maintenance.

Rush Hour Scenario

High-density scenario testing system robustness with many dynamic obstacles.

Technical Details

Achieved Performance

MetricValue
Collision Avoidance100% (0 violations)
Safety Distance0.60m maintained
Formation Tracking<0.1m error during avoidance
QP Solve Rate100% optimal solutions
Computation Time<1ms per robot
Real-time Performance60Hz control loop

Key Innovations

  1. Dynamic Obstacle Tracking - Real-time position updates from moving obstacles
  2. FixedCuboid Obstacles - Prevents robots from pushing obstacles (maintains safety)
  3. Robust QP Solving - Multi-solver fallback ensures reliability
  4. Safety Guarantees - CLF ensures convergence, CBF ensures collision-free

QP Formulation

Standard Form:

minimize    (1/2) * x^T * P * x + q^T * x
subject to  G * x <= h        (inequality)
            A * x = b         (equality)

Our Problem (per robot):

  • Decision variables: Control input u (2D), CLF slack variable
  • Objective: Minimize deviation from nominal control + slack penalty
  • Constraints:
    • CLF constraint (formation tracking with slack)
    • CBF constraints (one per obstacle - hard constraint)
    • Velocity bounds (box constraints)

Solve Time:

  • Typical: 0.3-0.8ms per robot
  • Worst case: <5ms (many obstacles)
  • Real-time capable at 60Hz

Scenarios

Pre-configured Scenarios

  1. Default - Basic warehouse with static and moving obstacles
  2. Corridor - Narrow passage navigation with adaptive spacing
  3. Intersection - Complex multi-obstacle intersection crossing
  4. Zigzag - Obstacles moving in zigzag patterns
  5. Emergency - Sudden stops and rapid direction changes
  6. Rush Hour - High-density obstacle environment

Moving Obstacle Patterns

  • Linear Motion - Straight-line trajectories
  • Circular Motion - Orbital patterns
  • Zigzag Motion - Alternating direction changes
  • Sudden Stop - Emergency braking scenarios
  • Inter-Obstacle Avoidance - Obstacles avoid each other

Safety Guarantees

Mathematical Foundation

Theorem (CBF Safety): If initially h(x₀) ≥ 0 and the CBF constraint ḣ + α·h ≥ 0 is satisfied at all times, then h(x_t) ≥ 0 for all t ≥ 0.

Proof Sketch:

If h(x_t) ≥ 0 and ḣ(x_t) + α·h(x_t) ≥ 0, then:
    ḣ(x_t) ≥ -α·h(x_t)

This differential inequality implies:
    h(x_t) ≥ h(x₀) · exp(-α·t) ≥ 0

Therefore: Robots that start in the safe set remain in the safe set forever (forward invariance).

Practical Implementation

  • Initialize robots far from obstacles (h > 0)
  • QP always finds feasible solution (if one exists)
  • CBF constraint is hard (no slack) → always enforced
  • Safety distance: 0.60m maintained at all times

Implementation Highlights

Critical Design Decisions

1. Dynamic Obstacle Reference:

  • Always reference live obstacle positions (not stale copies)
  • Real-time position updates from Isaac Sim sensors

2. FixedCuboid vs DynamicCuboid:

  • Use FixedCuboid to prevent robots from pushing obstacles
  • Maintains collision detection while preserving safety

3. QP Constraint Formulation:

  • Use box constraints (QP-compatible) not second-order cone
  • Enables fast, reliable solving with multiple solvers

4. Multi-Solver Fallback:

  • CLARABEL → SCS → ECOS → OSQP
  • Ensures 100% solve rate even with challenging scenarios

Moving Obstacle System

Inter-Obstacle Collision Avoidance:

  • Obstacles use repulsive forces to avoid each other
  • Creates realistic, dynamic scenarios
  • Prevents unrealistic obstacle overlaps

Results

Performance Metrics

Collision Avoidance:

  • ✅ 100% success rate across all scenarios
  • ✅ 0 collisions in extensive testing
  • ✅ 0.60m safety distance maintained consistently

Formation Control:

  • ✅ <0.1m tracking error during normal operation
  • ✅ <0.2m error during obstacle avoidance
  • ✅ Stable formation maintained throughout navigation

Computational Performance:

  • ✅ <1ms per robot average solve time
  • ✅ 60Hz control loop real-time capability
  • ✅ 100% QP solve rate with multi-solver fallback

Scenario Testing

All scenarios tested with:

  • Multiple obstacle patterns
  • Various convoy speeds
  • Different formation sizes
  • Edge cases (sudden stops, narrow passages)

Result: Zero collisions across all test scenarios.

Challenges and Solutions

Challenge 1: Stale Obstacle Data

Problem: Using copied obstacle positions at initialization caused stale references.

Solution: Always reference live obstacle positions from environment at each timestep.

Challenge 2: Obstacle Pushing

Problem: Dynamic obstacles could be pushed by robots, breaking safety guarantees.

Solution: Use FixedCuboid primitives that maintain collision detection but cannot be moved.

Challenge 3: QP Infeasibility

Problem: Some scenarios caused QP solver failures.

Solution: Implemented multi-solver fallback system (CLARABEL → SCS → ECOS → OSQP).

Challenge 4: Real-time Performance

Problem: QP solving needed to be fast enough for 60Hz control.

Solution: Optimized constraint formulation, used box constraints instead of SOCP, selected efficient solvers.

Future Work

Tier 1 Extensions (2-3 weeks)

  • Predictive Time-Varying CBF - Anticipate obstacle motion
  • Attention-Weighted Multi-Obstacle CBF - Prioritize critical obstacles
  • Social Force Integration - Model human-like obstacle behavior

Tier 2 Extensions (1-2 months)

  • Morphing Formations - Dynamic formation changes (line → diamond → split)
  • Game-Theoretic Navigation - Strategic obstacle interaction
  • Probabilistic CBF - Uncertainty quantification for sensor noise

Tier 3 Extensions (3-6 months)

  • Distributed Multi-Agent CBF - Decentralized control
  • Learning-Enhanced CBF - Neural-CBF for complex scenarios
  • Intent-Aware Semantic CBF - Understand obstacle intentions

Code Availability

The source code for this project is publicly available:

  • GitHub Repository: safe_convoy_isaac - Complete implementation with Isaac Sim integration, CLF-CBF controllers, scenario configurations, and visualization tools.

References

Control Theory

Control Barrier Functions:

  • Ames, A. D., et al. “Control barrier functions: Theory and applications.” European Control Conference (ECC), 2019.
  • Xu, X., et al. “Realizing simultaneous lane keeping and adaptive speed regulation on accessible mobile robot testbeds.” ASME Dynamic Systems and Control Conference, 2017.

Control Lyapunov Functions:

  • Artstein, Z. “Stabilization with relaxed controls.” Nonlinear Analysis: Theory, Methods & Applications, 1983.
  • Freeman, R. A., & Kokotović, P. V. “Robust nonlinear control design: state-space and Lyapunov techniques.” Birkhäuser, 1996.

Multi-Agent Systems:

  • Olfati-Saber, R. “Flocking for multi-agent dynamic systems: algorithms and theory.” IEEE Transactions on Automatic Control, 2006.
  • Wang, L., et al. “Safety barrier certificates for collisions-free multi-robot systems.” Robotics and Automation (ICRA), 2017.

Optimization

Convex Optimization:

  • Boyd, S., & Vandenberghe, L. “Convex optimization.” Cambridge University Press, 2004.

CVXPY:

  • Diamond, S., & Boyd, S. “CVXPY: A Python-embedded modeling language for convex optimization.” Journal of Machine Learning Research, 2016.

Acknowledgments

  • NVIDIA Isaac Sim Team - Simulation platform
  • Robotarium Project - Kinematic model inspiration
  • Aaron Ames’ Research Group - CBF theory foundations
  • CVXPY Developers - Optimization framework
← Back to Projects